Projeto utilizando lógica sequencial e combinacional: Garra automática

Olá a todos!

A postagem de hoje aqui no blog será um pouco diferenciada. Hoje iremos utilizar todos os nossos aprendizados para desenvolver um projeto bastante interessante. O projeto basicamente será uma garra responsável por levantar duas peças e levá-las até um local onde alguém possa retirá-las de lá. Este projeto não é focado em nenhum tipo de processo específico. Sendo assim, os processos que vem antes e depois da atuação da garra não são importantes (neste caso).

Para facilitar o entendimento deste projeto e deixar todo o processo mais visual, fiz uma animação simples de como todo o sistema deverá funcionar:

Para detectar as posições das peças serão utilizados sensores, enquanto para as posições da garra, serão utilizados sensores de fim de curso. A garra será movida por dois atuadores hidráulicos.

Posição dos sensores e fins de curso

Posições dos atuadores, assim como sua direção de atuação

Também faz parte do circuito um contador, responsável por permitir a movimentação da garra apenas após duas peças terem passado por ele.

Circulado na imagem está o local onde se encontra o circuito do contador

O circuito, como sempre, foi desenvolvido utilizando a ferramenta Proteus (é possível ampliar a imagem clicando nela):

Circuito responsável por efetuar os movimentos da garra

Para facilitar a compreensão, abaixo se encontra uma imagem com a utilidade de cada saída e cada entrada (é possível ampliar a imagem clicando nela):

Abaixo, encontram-se dois vídeos. No primeiro temos uma explicação de como funciona cada componente e como todo este circuito é capaz de fazer o projeto final funcionar. No segundo, temos uma animação da garra em conjunto com o funcionamento do circuito:

Explicação do funcionamento do circuito

Funcionamento do circuito em conjunto com a animação da garra

Como pudemos ver, o circuito ficou um pouco grande, mas ainda bastante simples. É importante comentar que este circuito foi desenvolvido apenas para mostrar como flip flops e portas lógicas podem funcionar bem em conjunto e, da forma apresentada aqui, não possui aplicações reais, principalmente por conta da falta de sistemas de segurança. Ainda existem várias melhorias que poderiam ser adicionadas, como por exemplo um sistema de alarme que seria ativado caso alguma peça se soltasse da garra no meio do caminho, caso o contador contasse mais de duas peças passando pela esteira ou caso o contador conte duas peças passando, mas após passado algum tempo os fins de curso nas garras não detectem que as peças chegaram, indicando que algo aconteceu no caminho da esteira. Isso para citar apenas alguns exemplo de melhoria que poderiam ser adicionadas a este sistema.

Enfim, espero que tenham gostado desta postagem (essa deu bem mais trabalho do que as outras, hehe) e do projeto. Espero que este blog tenha feito com que alguns de vocês, leitores, tenham se interessado pela eletrônica digital. Nos dias atuais, a eletrônica está presente em praticamente tudo, desde máquinas industriais até computadores pessoais e geladeiras. Acredito que a elétrica no geral serve para nos mostrar que a humanidade é incrível e que podemos ir longe quando trabalhamos em conjunto e com foco em nossos objetivos.

Espero que todos estes posts tenham sido interessantes. Até uma próxima, pessoal!

Contadores e registradores de deslocamento

Olá, pessoas!

Na nossa última postagem, tivemos um pouco de contato com os flip flops e aprendemos um pouco sobre seu funcionamento. Na postagem de hoje, vamos entender algumas de suas aplicações e como flip flops podem trabalhar em conjunto formando sistemas complexos e muito úteis.

Vamos começar falando sobre os contadores. Os contadores são componentes capazes de executar uma sequencia de contagem, geralmente em binário, BCD, Gray e códigos que envolvem números binários. Existem basicamente dois tipos de contadores: os síncronos e os assíncronos. Neste post, estaremos focando mais nos contadores assíncronos. De qualquer forma, ambos os tipos utilizam flip flops tipo T conectados em conjunto para fazer a contagem. Também é possível desenvolver um contador usando flip flops do tipo JK, visto que o flip flop T funciona como um JK com ambas as entradas (J e K) conectadas em um sinal alto.

Nos contadores assíncronos, o primeiro flip flop do conjunto recebe um sinal de clock, enquanto os outros flip flops recebem no clock o sinal vindo da saída barrada do flip flop anterior:

No vídeo a seguir é possível compreender o funcionamento do contador. A cada pulso de clock o contador aumenta um número em suas saídas. É possível notar que a saída do flip flop que recebe o pulso de clock diretamente contém o bit menos significativo.

A seguir, vamos compreender o funcionamento dos registradores. Assim como os contadores, existem vários tipos de registradores. Neste post vamos focar mais nos registradores de deslocamento. Este tipo de componentes também é feito utilizando flip flops, mas dessa vez são utilizados flip flops tipo D, diferente dos contadores, que utilizam flip flops tipo T. Também é possível fazer registradores usando flip flops JK, visto que os flip flops D podem ser feitos utilizando flip flops do tipo JK, ligando a entrada J e K em um mesmo sinal e invertendo o sinal da entrada K.

Os registradores são capazes de coletar um conjunto de dados e guardá-los dentro de si. Estes dados podem ser fornecidos para o registrador em série ou em paralelo. O registrador que veremos hoje possui a entrada de dados em série e a saída em paralelo.

Este tipo de registrador se chama "registrador de deslocamento" pois o bit adicionado no registrador a cada pulso de clock faz com que os bits que já estão guardados no registrador se movam para a frente. No vídeo abaixo é possível ver este processo:

Como pudemos ver neste post, os flip flops são muito úteis para diversas funções e podem fazer tarefas incrivelmente complexas e importantes quando trabalham em conjunto. Isso até lembra um pouco a nossa sociedade, não é mesmo? Também é possível fazer circuitos parecidos com os registradores de deslocamento utilizando relés, por exemplo, mas é muito mais complexo e ineficiente do que a forma utilizando flip flops:

Enfim, este foi o post de hoje. Espero que tenham gostado e que tenha sido interessante. Até a próxima!

Podcast sobre flip flops

Olá a todos!

No post de hoje, veremos um pouco sobre os chamados flip flops e também um pouco sobre o latch, que é bastante parecido com os flip flops e, na realidade, faz parte da construção dos mesmos. Porém, no post de hoje, faremos algo ligeiramente diferente. Ao invés de um post com um texto enorme e cansativo, hoje teremos uma postagem em forma de podcast. Porém, entendo que muitas vezes se torna difícil visualizar e imaginar o que se está sendo dito em um áudio e por este motivo, serão disponibilizadas algumas imagens neste post, para que se possa ter uma referência durante o podcast.

Para fazer uma introdução rápida, um flip flop é um componente muito utilizado como memória, visto que é capaz de guardar um único bit dentro de si. Circuitos capazes de guardar informações em sua “memória” e que podem variar sua saída não apenas dependendo dos sinais de entrada, mas também dos sinais de saída anteriores são chamados de circuitos sequenciais. Existem vários tipos de flip flops, mas todos eles têm origem em um componente chamado “latch”. Este componente é muito simples, porém muito útil. Se trata de um circuito que possui duas entradas: uma chamada “set” e outra chamada “reset” e duas saída: Q e Q', onde Q' é o sinal de Q invertido. Ao adicionar um sinal na entrada “set”, a saída Q assume valor 1 e a saída Q' assume o valor 0. Já quando a entrada reset recebe um sinal, o inverso acontece. Q se torna 0 e  se torna 1. Veja abaixo uma imagem do circuito responsável pelo funcionamento deste componente:

O flip flop tem sua origem neste mesmo componente. A diferença é que o flip flop depende de um sinal chamado clock para que as suas entradas se modifiquem. Mesmo que uma das entradas possua um sinal, caso o clock não esteja ativo, o estado das saídas não se modifica. É muito importante lembrar que existem vários tipos de flip flops. No mini podcast a seguir, iremos ver o funcionamento de vários tipos e, para facilitar o entendimento, abaixo temos as imagens referentes a cada um dos tipos:

Flip Flop RS síncrono

Flip Flop do tipo T

Flip Flop do tipo D

Flip Flop com preset e clear

A seguir, fique com o podcast. Para fazer o download clique nas três bolinhas ao lado do controle de volume do player (recomendo que faça o download para ouvir, visto que o player utilizado não é muito eficiente):

Multiplexadores e demultiplexadores

 

Olá a todos!

No post de hoje, iremos conhecer os multiplexadores e os demultiplexadores. Embora o nome seja um pouco assustador, na realidade, estes componentes são muitos simples. Neste post, iremos entender o funcionamento dos multiplexadores e dos demultiplexadores, veremos algumas aplicações e também como podemos desenvolver ambos os componentes utilizando nossos conhecimentos de portas lógicas e circuitos lógicos.

Vamos começar o nosso estudo pelos multiplexadores. Como dito anteriormente, embora o nome seja complexo, se tratam de componentes muito simples. Sendo assim, vamos começar já simplificando este nome complexo: multiplexadores podem ser chamados de mux e demultiplexadores podem ser chamados de demux. Os multiplexadores (mux) nada mais são do que circuitos responsáveis por receber sinais elétricos de várias fontes diferentes na entrada e emitir estes sinais por uma única saída. Podemos imaginar que se trata de um componente com diversas entradas e com uma chave conectada a um fio, que passa por todas as entradas, conectando uma por vez ao fio de saída. A seleção das entradas é feita utilizando um código binário:

 

Este exemplo é muito interessante para compreender o funcionamento dos multiplexadores, porém, não representa a realidade de seu funcionamento. O multiplexador, na realidade, faz uso de portas lógicas AND, OR e NOT para funcionar. Para entendermos melhor, nada melhor do que usar todos os nossos conhecimentos adquiridos até hoje sobre circuitos lógicos e desenvolver um multiplexador do zero.

Primeiramente, devemos montar a tabela verdade. Iremos desenvolver um multiplexador com 4 entradas, então precisaremos de 4 valores diferentes para fazer a seleção das entradas. Para isso, podemos usar dois bits, visto que 2² = 4. Obs: o número de entradas do multiplexador deve ser igual a 2 elevado ao número de bits utilizado na seleção. Logo, se fossemos usar 4 bits para a seleção, teríamos um mux com 16 entradas (2^4 = 16).

Porém, estamos trabalhando com 2 bits de seleção, o que nos dará 4 entradas:

Com isso, podemos desenvolver nossa tabela verdade. Temos dois bits de seleção, logo, nossas opções para a seleção serão: 00, 01, 10 e 11. Cada uma dessas opções será responsável por selecionar uma saída:

B1	B2	Selecionar
0	0	A
1	0	B
0	1	C
1	1	D

Utilizando os conhecimentos adquiridos em posts anteriores, podemos entender o seguinte. A entrada A é igual a B1’ AND B2’, a entrada B é igual a B1’ AND B2, C é igual a B1 AND B2’ e, finalmente, D é igual a B1 AND B2. Todos esses sinais serão direcionados à mesma saída, logo, precisaremos de uma porta OR no final do circuito. Com isso, teremos a seguinte expressão: 

Agora, para montar o circuito, devemos associar cada entrada com sua combinação, para que apenas a entrada desejada passe para a saída:

Agora que já temos o circuito montado utilizando a lógica booleana, podemos passar para um circuito real. O circuito ficará parecido com isso:

Fazendo a simulação, podemos perceber que este circuito apenas permite a passagem da entrada selecionada para a saída. Se a saída D, por exemplo, estiver selecionada (com o código 1 1 na seleção), os bits de todas as outras entradas não poderão chegar até a saída. Apenas o bit D será capaz de acender o LED azul ao final do circuito (se você é como eu e gosta de estudar ouvindo música, não se preocupe. O vídeo não tem som):

 

Porém, agora surge a pergunta: qual seria a utilidade de um circuito desses? Muitas vezes, no dia a dia, se torna ineficiente, custoso e muitas vezes impossível utilizar um número muito grande de cabos para transportar sinais de um ponto ao outro de um local. Nestes casos, um mux se torna muito útil. Porém, na saída do mux, temos apenas uma saída, com bits saindo o tempo todo. Se refletirmos um pouco, a informação inicial iria se perder na saída do mux, visto que uma informação de 4 bits se torna um conjunto de bits saindo por apenas um fio. É neste ponto que entra o demultiplexador (ou demux). Este componente é responsável por fazer o processo inverso do mux: pega uma entrada e divide para várias saídas. O circuito é muito simples. Precisamos apenas retirar as portas OR e ligar as portas AND direto na saída. As quatro entradas também irão dar lugar a uma entrada única:

 

Na simulação do circuito, a entrada foi trava em nível lógico 1 e, usando os bits de seleção, a saída foi sendo modificada:

 

Estes dois componentes geralmente são utilizados em conjunto, como podemos ver no GIF abaixo:

 

Para que o funcionamento seja perfeito, é necessário que os bits de seleção estejam sincronizados, pois, caso não estejam, é possível que o sinal de uma entrada do mux saia na entrada errada do demux.

Por hoje, foi isso. Como dito no início do post, este é um assunto bastante simples, embora pareça complexo de início. O importante é compreender os detalhes e o funcionamento completo do sistema.

Enfim... espero que tenham achado este post interessante. Até a próxima!

Codificadores e decodificadores (com desenvolvimento de um codificador decimal/BCD)

Olá a todos! Espero que estejam todos bem.

No post de hoje veremos um assunto muito interessante: codificadores e decodificadores.

Os codificadores e os decodificadores são circuitos eletrônicos que possuem funções muito parecidas. Na realidade, a diferença entre os dois é praticamente nula e se encontra principalmente na perspectiva. Este conceito pode parecer bastante confuso no início, porém irá fazer mais sentido no decorrer neste post. Um codificador é um circuito responsável por transformar um código conhecido em um código desconhecido, enquanto um decodificador faz o processo contrário (transforma um código desconhecido em um código conhecido). É neste ponto que entra a parte da perspectiva. Vamos imaginar um circuito que transforma números decimais em números binários. Do ponto de vista humano, se trata de um circuito codificador, pois faz a conversão de números decimais (muito utilizado e conhecido pelos seres humanos) em números binários (muito conhecido e utilizado por computadores). Porém, do ponto de vista do computador, se trata de um circuito decodificador, pois transforma os decimais (desconhecidos para os computadores) em binário. Neste exemplo, parece ser bem claro que o circuito se trata de um codificador, pois conhecemos muito bem os números decimais e não temos tanta proximidade com códigos binários, porém, ao trabalhar com códigos que não costumam ser muito utilizados por humanos, esta confusão fica ainda mais clara. Por este motivo, costumamos considerar os codificadores como sendo os componentes que tem mais entradas, enquanto o decodificador é o componente com mais saídas.

Anteriormente já foi mencionado o exemplo de conversores responsáveis por fazer a conversão de números decimais em binários. Anteriormente neste mesmo blog, tivemos a oportunidade de aprender a fazer este tipo de conversão manualmente. Também vimos, a alguns posts atrás, como desenvolver circuitos eletrônicos. Juntando estes conhecimentos, se torna possível desenvolver um circuito responsável por fazer este processo de conversão automaticamente. Neste post em específico, será criado um circuito responsável por transformar números decimais em binários de 4 bits, podendo converter números de 0 até 9. Este código é chamado de BCD e já foi apresentado em posts anteriores deste blog.

O primeiro passo é desenvolver nossa tabela verdade. Ela ficará assim:

E	B1	B2	B3	B4
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1

Podemos perceber que temos apenas uma entrada e várias saídas. Pode parecer complicado no início, mas na realidade, isso irá facilitar nosso trabalho. Podemos perceber, por exemplo, que a entrada “0” não aciona nenhuma saída. Sendo assim, não precisaremos ligá-la em nada. Também é possível notar que a saída “B4” é acionada apenas pelas entradas 1, 3, 5, 7 e 9. Sendo assim, podemos usar uma porta OR conectada a essas entradas e com a saída conectada em B4, pois qualquer uma dessas entradas deve acionar a saída B4.

 A saída B3 deve ser acionada quando as entradas 2, 3, 6 e 7 receberem sinais, então podemos ligar estas saídas a algumas portas OU também.

 Repetiremos este processo para todas as entradas. Ao final do processo, este é o circuito encontrado:

 

É possível perceber que a entrada “0” não está conectada a nada. Neste exemplo, foram usadas portas OU de duas e três entradas, para que seja possível perceber como várias portas lógicas podem ser usadas em conjunto, apresentando a mesma função que uma porta com mais entradas. Podemos perceber que este circuito é capaz de executar sua função corretamente:

 

Como podemos ver, com todos os conhecimentos que acumulamos até agora, já é possível criarmos coisas bastante interessantes. Com este código BCD da saída, podemos utilizar, por exemplo, outro codificador para mostrar o número decimal selecionado em um display de 7 segmentos, ou então utilizar um somador para somar vários valores decimais que seriam transformados em binário utilizando um circuito parecido com este.

Como sempre, espero que este post tenha sido interessante. Até a próxima! :)

Somadores

 Olá a todos! No último post aqui do blog, pudemos ver um pouco mais sobre conversão numérica e circuitos lógicos. Porém, creio que seja interessante demonstrar um pouco melhor alguns usos para essas conversões e circuitos lógicos e como elas podem ser usadas para facilitar a vida do ser humano. Neste post, iremos ver um pouco sobre somadores, que nada mais são do que circuitos lógicos capazes de fazer a soma de números binários.

A soma de números binários é muito parecida com a soma de decimais que já estamos acostumados. A diferença, porém, é que, ao invés de termos dez algarismos, agora temos apenas dois. Vamos observar um exemplo:

Neste exemplo, temos a soma de dois números decimais. Observe que, quando somamos oito com dois, obtemos o número dez. Isso faz com que o número 1 (de 10) seja "carregado" para o algarismo seguinte, fazendo com que em seguida seja feita a soma de 2 + 2 + 1 (que veio da soma anterior). Agora vamos analisar a mesma soma feita com número binários. Fazendo a conversão de decimal para binário, vamos encontrar os seguintes números para nossa soma: 

Estes números equivalem a 28+22, porém desta vez em binário. Caso haja alguma dúvida na parte de conversão de decimais em binário, é possível encontrar neste mesmo blog um post sobre conversão de unidades. Podemos perceber que a soma é muito parecida, porém, agora, quando temos a soma de 1 + 1, temos o número 1 sendo "carregado" para a próxima parte da soma. Isso acontece pois em binário, 1 + 1 daria "1 0" (2 em decimal), algo muito parecido com o 8 + 2 na soma com decimais, onde teríamos o surgimento de um número com 2 algarismos (10). Como estamos trabalhando com números binários, se torna possível usar portas lógicas para desenvolver circuitos que fazem a soma automaticamente, acabando assim com a necessidade de fazermos somas manuais.

Para desenvolvermos um circuito lógico, iremos usar as mesmas técnicas aprendidas em nosso último post. Para começar, vamos desenvolver uma tabela verdade. Primeiramente, vamos desenvolver um circuito somador capaz de fazer a soma de uns e zeros e de "carregar" um número, caso a soma seja entre dois uns. Para o 1 "carregado", daremos o nome de Cout (carry out). A tabela verdade deste circuito ficará assim:

A	B	Cout	Soma
0	0	0	0
1	0	0	1
0	1	0	1
1	1	1	0

Analisando esta tabela verdade, podemos notar algo interessante: a coluna "Cout" funciona como uma porta "AND". Perceba que a saída apenas é 1 quando as duas entradas são iguais a 1. Observando esta tabela verdade, também é possível notar algo interessante sobre a coluna "soma": ela funciona como uma porta "XOR". Caso seja necessário, é possível rever o funcionamento de cada porta lógica em um post do blog chamado "portas lógicas e seus circuitos".

Sendo assim, o desenvolvimento deste circuito se torna bastante simples: a saída "soma" ficaria ligada a uma porta XOR e a saída Cout ficaria ligada a  uma porta AND. Observe:

Este circuito faz exatamente o que precisávamos. Porém ele não está completo, pois ainda não tem como receber o número carregado de somas anteriores. Caso este circuito seja o responsável por fazer a primeira soma de um conjunto, ele pode ser útil, mas caso ele esteja no meio de um processo de soma, ele seria falho justamente por não receber números carregados de somas anteriores. Por este motivo, este circuito é chamado de "meio somador" ou "half adder".

Caso o circuito seja responsável por fazer a primeira soma, ele funciona perfeitamente

Para permitir que o circuito receba números carregados de uma soma anterior, precisamos adicionar mais uma entrada. A tabela verdade seria algo assim:

Para desenvolver um circuito utilizando esta tabela verdade, podemos usar algumas técnicas. É possível desenvolver uma expressão booleana utilizando os resultados das saídas e simplificá-la para obter um circuito ou também é possível utilizar a lógica para desenvolver o circuito. Na tabela, podemos ver que todas as saídas que não envolvem Cin (carry in) na entrada continuam iguais ao circuito anterior. Então tudo o que precisamos fazer é adaptar o circuito para que o Cin  cumpra seu papel. Podemos perceber então o seguinte: 

A	B	Cin	Cout	Soma
0	0	1	0	1
0	1	1	1	0
1	0	1	1	0
1	1	1	1	1

Com isso podemos perceber o seguinte: a saída "soma" fica invertida quando adicionamos o "Cin". Uma forma interessante de inverter a saída apenas quando tivermos um sinal no Cin é utilizando uma porta "xor":

Agora, sempre que tivermos um sinal vindo de Cin, o sinal vindo da primeira porta xor será invertido.

Na parte de Cout, precisamos agora adicionar algumas portas para que o funcionamento seja o que esperamos. Podemos perceber que o último caso (A = 1, B = 1 e Cin = 1) já está feito, visto que, de qualquer forma, quando A e B forem iguais a 1, Cout será igual a 1. O mesmo ocorre quando A e B são iguais a 0. Porém, agora precisamos adaptar o circuito para que a saída Cout seja igual a 1 quando A ou B forem iguais a 0, e Cin for igual a 1. Para isso, podemos fazer o seguinte: se A XOR B = 1 e Cin = 1, o Cout também será igual a 1. Perceba que precisaremos de apenas mais uma porta AND, visto que já temos uma porta XOR recebendo A e B.

Agora temos duas condições para que o Carry Out seja 1: quando A e B forem 1 e quando A XOR B e Cin forem 1. Sabemos que quando qualquer uma dessas condições for verdadeira, Cout será 1. Sendo assim, precisamos apenas colocar uma porta OR na saída. 

Pronto! Temos agora o nosso circuito somador. Dessa forma é possível fazer a soma de binários de forma automática.

Como sempre, deixo abaixo o link de um vídeo muito interessante sobre somadores que foi utilizado como fonte para algumas das informações contidas neste post (assim como o desenvolvimento do circuito sem utilização de álgebra de Boole):

Learn how computers add numbers and build a 4 bit adder circuit - YouTube (em inglês).

Espero que tenham gostado deste post. Até a próxima :-)

Circuitos lógicos (utilizando exercícios do livro de Ronald J. Tocci)

Olá a todos! Espero que estejam tendo um bom dia.

Como todos sabemos, este é um blog sobre circuitos lógicos. Porém, algumas pessoas podem se questionar o motivo de, até o presente momento, não termos montado nenhum circuito lógico propriamente dito. Já tivemos posts sobre as portas lógicas (que são a base dos circuitos lógicos), sobre codificadores, softwares para simulação e até sobre conversão numérica, mas não vimos como um circuito lógico realmente funciona. Por este motivo, hoje faremos a simulação de alguns circuitos básicos e iremos entender seu funcionamento. Antes de iniciar, é interessante recapitular alguns conceitos vistos em posts passados, pois estes conceitos são bastante importantes para a compreensão de algumas aplicações dos circuitos lógicos. Para isso, será usado como base o livro "Sistemas Digitais" (11ª edição) de Ronald J. Tocci.

Primeiramente, vamos relembrar como são feitas conversões de unidades. Sempre que temos um número binário, por exemplo, podemos convertê-lo para decimal, assim como podemos converter um número decimal em binário. Como já existe um post no blog detalhando essas conversões, irei apenas comentar sobre as conversões e mostrar alguns exemplos.

No exercício 2-1 a) do livro do Tocci, encontramos nosso primeiro desafio: Converter o número 10110 em decimal. Quando nos lembramos da forma utilizada para converter números binários em decimal, podemos perceber que esta é uma tarefa bastante simples. Basta lembrar que o bit menos significante (mais a direita) vale 2 (base do número binário) elevado a 0 (posição do bit) e o bit mais significante (mais a esquerda) vale 2 elevado a 4 (pois este é um número de 5 bits e, considerando que a primeira posição é o 0, a última posição fica sendo o 4).

Agora, basta multiplicar o número correspondente a potência pelo número binário:

Agora, somamos os resultados:

E pronto! O número 10110 corresponde ao número 22!

Agora, devemos nos lembrar que o contrário também é possível. Podemos converter número decimais em números binários. Para este exemplo, irei utilizar o exercício 2-1 b) do livro do Tocci, onde devemos converter o número 13 em binário. Observe que agora precisaremos fazer várias divisões sucessivas por 2 e observar sempre o valor do resto para chegar ao número binário correspondente. Lembrando que, caso haja alguma dúvida sobre esta conversão, o primeiro post deste blog explica com mais detalhes (e com um vídeo) sobre o processo de conversão.

Para começar, vamos dividir o número 13 por 2. Teremos como resultado o número 6 e resto 1:

Depois, faremos a divisão por 2 até encontrarmos o resultado 1 ou 0:

Pronto! Agora só precisamos pegar o último resultado (que no caso é 1), considerar ele o bit mais significativo e colocar os restos como bits menos significativos (respeitando a ordem em que eles aparecem):

Com todas essas informações, já podemos fazer algo um pouco mais diferenciado. Em um dos posts anteriores deste blog, foram mostrados alguns códigos diferenciados. Um deles foi o BCD, que representa números decimais de 0 a 9 utilizando grupos de 4 bits. Este código é muito utilizado em displays de 7 segmentos. Lendo o livro do Tocci, me deparei com um exercício muito interessante e que tem bastante relação com a postagem de hoje. O exercício 2-19 pede para que seja feita a conversão do número 47 para o código BCD. A primeira vista, este pode parecer um exercício muito complicado, visto que até agora foram feitas apenas conversões de binário para decimal e de decimal para binário. Porém, precisamos nos lembrar que o código BCD nada mais é do que a representação dos números decimais usando 4 bits, ou seja, esta conversão nada mais é do que uma conversão de decimal para binário. Porém, existe outro problema: o código BCD vai apenas de 0 a 9 e 47 é um número bem maior do que 9. Novamente, precisamos nos lembrar de como funciona o código BCD. Neste tipo de código, vamos representar cada algarismo como um número binário de 4 bits. Ou seja, vamos converter o 7 em um binário de 4 bits e depois o 4. A resolução é a seguinte:

Sendo assim, o número ficaria: 0100 0111. Lembrando que sempre precisamos representar os números em BCD com 4 bits, ou seja, precisamos adicionar zeros a esquerda caso o número tenha menos de 4 bits. Este exercício é interessante pois existem circuitos lógicos responsáveis por transformar números binários em BCD para a utilização em displays de 7 segmentos, que por sua vez mostram os números em decimal. Neste exercício vimos, matematicamente, como é feito o processo contrário e ao final deste post, deixarei um link para um vídeo (infelizmente em inglês) onde é possível ver com mais detalhes o funcionamento de um circuito deste tipo.

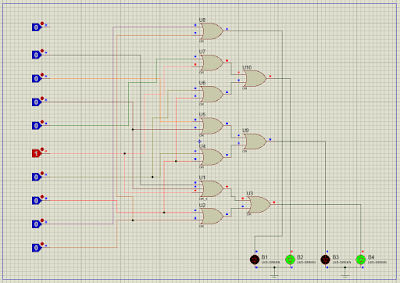
Agora, vamos finalmente para os circuitos lógicos. Os circuitos lógicos são circuitos que fazem uso de portas lógicas para executar certas tarefas. Para desenvolver circuitos lógicos é utilizada a álgebra de Boole. Na álgebra de Boole, as portas AND funcionam como uma multiplicação (caso um dos sinais recebidos seja 0, o resultado da operação é 0) e as portas OR funcionam como uma soma (caso um dos sinais seja 1, o resultado seria 1). Esta ferramenta é muito importante para facilitar a construção de circuitos lógicos. Para entender melhor este assunto, vamos começar com circuitos lógicos montados e iremos encontrar a expressão booleana correspondente ao circuito. Depois disso, iremos partir da expressão booleana e com isso teremos as informações necessárias para montar o circuito. Abaixo, podemos ver um exemplo utilizando o exercício 3-12 do livro do Tocci.

Circuito feito usando o programa Proteus

Devemos nos lembrar que as portas AND são consideradas multiplicações a as portas OR são consideradas somas. Sempre que tivermos um sinal invertido (com a porta NOT, por exemplo), o sinal será representado com uma barra em cima da letra correspondente. A primeira entrada deste circuito será chamada de A, a segunda de B e a terceira de C. Sendo assim, a expressão booleana para este circuito seria:

Com isso, se torna muito mais fácil analisar qual seria a saída se A, B ou C fossem 1 ou 0. Bastaria substituir na equação.

Agora, iremos fazer o oposto. O exercício 3-16 a) do livro do Tocci nos dá a seguinte expressão: 

A partir desta expressão, precisamos encontrar o circuito que a geraria. Para isso, inicialmente, vamos perceber que a expressão inteira está barrada (com a barra em cima, representando que ela está inteira invertida. Isso significa que temos que ter uma porta inversora na saída do circuito. Podemos perceber também que a expressão é uma multiplicação entre AB e (C+D). Sendo assim, sabemos que devemos usar uma porta AND no fim do circuito. É importante lembrar que existe uma porta lógica chamada NAND, que nada mais é do que uma porta AND com a saída barrada (invertida). Esta porta será perfeita neste caso, visto que precisamos de uma porta AND com a saída barrada:

Agora, vamos pensar no resto do circuito. Temos a soma C+D. Somas são feitas nas portas OR:

É importante notar que a saída desta porta OR não é barrada. A expressão final completa (AB*(C+D)) é barrada, porém as partes individuas neste caso não são. Para a soma C+D ser barrada, seria necessário que a expressão fosse a seguinte:

Dando continuidade, agora precisamos apenas multiplicar A e B e o resultado da operação feita na porta OR (C+D). Sendo assim, o circuito final ficaria assim:

Então já pudemos ver como é feita uma expressão booleana usando um circuito pronto e como é feito um circuito usando uma expressão booleana pronta. Porém, no segundo exemplo, de onde veio a expressão booleana? No primeiro exercício, ela veio do circuito, mas no segundo, não havia nenhum circuito para buscar a expressão. É aí que entra a tabela verdade. Em um post anterior deste blog, onde estudamos sobre portas lógicas, pudemos ver um pouco sobre as tabelas verdade, onde colocamos os valores de entrada em uma coluna e os valores desejados de saída em outra. A tabela verdade também é muito utilizada para desenvolvimento de circuitos lógicos. Para entender melhor, vamos usar mais um exemplo do livro do Tocci :

Para facilitar nosso trabalho, podemos fazer uma tabela verdade:

    

Podemos notar que temos apenas um ponto onde queremos que a saída seja 1. Para representar este ponto algebricamente, vamos representar as letras que irão assumir 1 como variáveis comuns (A e C) e vamos representar a letra B (que deverá ser 0) como B barrado:

   

Como podemos ver, apenas uma situação satisfaz a nossa saída, e ela é A*B'*C (B' sendo o B barrado). Caso mais de uma combinação fornecesse a saída desejada, deveríamos somar todas as combinações possíveis (usaríamos portas OR no circuito).

Usando a expressão que conseguimos com a tabela verdade, chegamos ao seguinte circuito:

Por hoje é isso. Como prometido, segue abaixo o vídeo do display de 7 segmentos, onde é desenvolvido um circuito que converte códigos binários em um código hexadecimal que é mostrado no display, para representar todos os 4 bits do código binário (diferente dos código BCD, que vai apenas de 0 a 9). Com este vídeo, é possível ver como podem ser desenvolvidos circuitos muito complexos utilizando apenas portas lógicas:

"Designing a 7-segment hex decoder": 

https://www.youtube.com/watch?v=7zffjsXqATg&ab_channel=BenEater

Enfim, este post foi bastante longo, mas este é um assunto bastante complexo e que exige um certo tempo para ser explicado em detalhes. Como sempre, espero que este post tenha sido útil. Até a próxima!